| 07030344255 | ASK US |
MATHS INDUCTION
Nothing holds more mystery in secondary school math than the students’ foundation in elementary mathematics. And if they must excel in their mathematics, understanding the basic concepts of certain rules is all but nonnegotiable. The concept of equation is one of such rules.
Although this website focuses on SSCE, UTME and Post-UTME candidates, but because their foundation in elementary math either holds a solid platform for their take-off, or an impatient vacuum in their head, we leave nothing to chance. And so we assume here that every student visiting this page, especially for the first time, has a rather frail foundation in Mathematics.
We hope you oblige to this surmise for a successful induction into the science of mathematics, as you get set for the loads of math packages we have right here on this website for you. You may as well skip this page (if you think you have proof to). But we welcome you to surf this website for other interesting contents. Otherwise, relax and give yourself to the expository spelt out here on this page.
What you'll find in this tutorial
BIG NEWS!
What is Mathematics?
Think of mathematics, think of your everyday transactions, like buying biscuit from a shop, paying the cab driver who’d driven you to your bus-stop, and so on. Mathematics however is defined as a science that deals with the logic of quantity, shape and arrangement.
It is the quantity in this definition that bargains for mathematics presence in our everyday lives. Quantity here refers to amount (how much there is or how many there are of something). And numbers, of cause, are used to represent this amount.
If supposed mathematics was partitioned into three phases of morning, afternoon and evening sections, the morning phase would be the explicit or elementary stage (which is the nursery/primary education), while the afternoon and the evening phases would comprise mostly of the implicative parts, with boundless concomitance of the connotations of the elementary stages. Secondary school mathematics would occupy the early periods of the afternoon phase.
In my years of experience as a senior secondary school mathematics teacher, I’ve come to realize the situation in which many senior school students find themselves is one expressed by the famous wit which has it that, whenever a man wakes-up is his own morning. Many of these secondary school students went through their morning periods in drowsiness due to the inability of the young mind to comprehend the will of purpose. Children would always be children though. But the push required to get them on track then hadn’t come from their parents or otherwise had been applied inadequately. So I take nothing away from them.
But the good news is, help is right here on this page! We have put together a comprehensive highlights of the morning phase of mathematics for your summary. And deeply immersed in this spotlight is an expository on equations which cannot be overemphasized in your arithmetic. So let’s get the ball rolling, if you are ready! Shall we?
The Elementary of Mathematics
Introduction
Mathematics in its natural state is all about numerals; 0, 1, 2, 3, 4,….In elementary mathematics, all the students ever did are more or less addition, subtraction, multiplication and division on numerals. For example;
Simple! But when alphabets are involved, it is mainly for counting, adding or subtracting. For example;
| x x x x | How many x are there? 4x. |
| x x x y y y y | How many? 3x and 4y |
| x + x + x - x | What is the answer? 2x |
| x + x + y + y + y | What is the answer? 2x + 3y |
Terms of Mathematical Expressions
| 2 + 3 | There are two terms in this expression. The two terms are 2 and 3 |
| x + 2y - m | There are three terms; x, 2y and -m. Note that the signs follow the terms. Thus the 3rd term has a negative sign |
| 3xy -y + m - 4 + y² | There are five terms; 3xy, -y, m, -4 and y². Note that y and y² are two different terms. |
Note: a term is either positive (+) or negative (-). When negative, its sign(-) is made visible at all times.
Terms which are similar are called like terms. For example
| 2x + x + 5y - 3x + y + x | There are two like terms in the expression. And they are x and y |
| 4x – 6 – 2y + 1 + 3m + y | There are four like terms here; x, y, m and the numerals (-6 and 1). We could bring like terms together to compress the expression to, 4x–6+1–2y+y+3m which then gives 4x–5–y+3m |
| 2y + 8 + √2 – x – 1 + √3 | There are six like terms in the expression; 2y, x, √2, (8 and -1) and √3. Note that √2 and √3 are different terms by surd. They are called surd because their roots do not give whole numbers. The expression could be compressed to 2y–x+7+√2 + √3 |
Operations on Terms of an Expression
Addition (+)
Only like terms are added or summed up together. As we saw in our earlier example where, x + x + y + y + y gave 2x + 3y.
Unlike terms are never added together in mathematics.
Subtraction (–)
Subtraction, Just as addition, is performed only on like terms. On no condition does it apply to unlike terms.
For example, given the expression,
2x – 4y – x – 3y – y – m – √5 – √3 – 3√5
we group like terms, and then subtract
2x – x – 4y – 3y – y – m – 3√5 – √5 – √3
x – 8y – m – 4√5 – √3
Note: Subtraction from a negative term gives addition, and the result retains the negative sign. To understand this better, lets take a look at the number line;
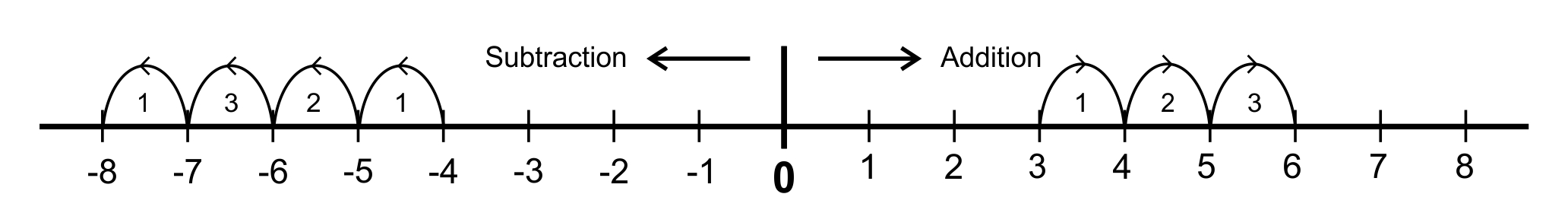
Remember this?
To add, we move to the right the number of times corresponding to the addition. For example, 3 + 3, we move three steps to the right from 3, as shown above. And that gives 6.
For subtraction, we move to the left to the number of times the subtraction. For example, –4 – 3,
we move three steps to the left from –4, and that gives –7. Then –7 – 1, gives – 8.
Thus;
–4y – 3y – y
gives –7y – y
which then yield –8y
Multiplication (X)
In mathematics, multiplication is supreme. It applies to all terms of a mathematical expression, irrespective of whether they are like terms or not.
Before we take some examples on multiplication, lets get acquainted with the word, coefficient.
Coefficient is simply the numerical value of a given term, i.e, the number in front of the term. But when this numerical value stands alone, it is called a constant and not a coefficient. For example
y → the coefficient of y is 1
3y → the coefficient of y is 3
–x → the coefficient of x is -1 (–1 X x = –x)
5 → this is a constant and not a coefficient
√6 → the coefficient of the surd is 1 (1 X √6 = √6)
Thus coefficient, literally, is the numerical value of an aphabet used in mathematics.
Note: Every alphabet used in mathematics has a coefficient. But the coefficient is not written when it is 1. It makes no sense writing 1y or 1√6 because it is the same as y or √6.
...back to multiplication.
Below are some examples on multiplication
| x X y | Answer: xy |
| 2 X y | Answer: 2y |
| 3 X 2m | Answer: 6m |
| y X y | Answer: y² (when like terms multiply themselves, the result is expressed to the power of the number of the multiplying terms. |
| 4 X 4 X 4 | Answer: 4³ which is equally 64 |
| 2m X m X m | Answer: 2m³ the coefficients and the alphabets multiply themselves separately (2X1X1)(mXmXm) which then yields 2m³ |
| √7 X √7 | Answer: 7 when like surds multiply themselves, the root vernishes. Verify with a calculator. Punch √7 X √7 and see. |
| √2 X 3√5 X m X 2y | Answer: 6√10my that is (1X3X1X2)(√2X√5XmXy) which yield (6)(√2X5XmXy) which the yield 6√10my |
| 3m X 2y X n X y | Answer: 6mny² that is (3X2X1X1)(mXnXyXy) which is 6mny² |
Division (÷)
Division simply means to divide. It is dividing the numerator to the number of equal parts stated by the denominator. For example:
10 ÷ 2 simply means to divide 10 into two equal parts. And that would give 5 (i.e, 5 + 5 = 10).
18 ÷ 3 divide numerator into three equal parts. And that would give 6 (i.e, 6 + 6 + 6 = 18)
2 is a factor of 10 (So as 3 is a factor of 18). Factors of a term are numbers which can divide it to give whole numbers. The factors of 10 are 1, 2 and 5. While that of 18 are 1, 2, 3, 6 and 9.
1 and 2 are common to both 10 and 18. But because 1 is a factor of every number, its place as a factor is practically neglected. Thus 2 is the common factor of 10 and 18. It is also the Lowest Common
Factor (LCF) as well as the Highest Common Factor (HCF) of 10 and 18.
HIGHEST COMMON FACTOR (HCF): This is the highest factor common to two or more terms. Below are some examples:
|
12 → factors: 2,3,4 and 6, 16 → factors: 2,4 and 8 24 → factors: 2,3,4,6,8 and 12 |
The highest common factor of all three is 4. |
|
27 → factors: 3 and 9 18x → factors: 2, 3, 6, 9, x, 2x, 3x, 6x and 9x 45 → factors: 3,5,9 and 15 |
The highest common factor of all three is 9. |
Knowing the HCF of an expression is key to solving problems in factorization.
Mixed Operations:
With mixed operation comes the essence of BODMAS (Bracket Of Division, Multiplcation, Addition and Subtraction). Study the following examples:
Example 1:
3x – y – 5 – x + 7y + √3 + 2 + √2 + 2√3
Answer: 2x + 6y – 3 + √2 + 3√3
How? We collect like terms, 3x – x + 7y – y + 2 – 5 + √2 + 3√3 + √3
and this yied the answer, 2x + 6y – 3 + √2 + 3√3
Example 2:
m + 2 + (y X m X y) – (√5 – √3 + 4√5)
Answer: m + 2 + my² – 5√5 + √3
How? By BODMAS, we clear the brackets. But lets collect like terms first,
m + 2 + (y X y X m) – (√5 + 4√5 – √3)
m + 2 + y²m – (5√5 – √3)
now we clear the brackets by multiplying through with the coefficients in front of them, to obtain the answer
m + 2 + y²m – 5√5 + √3
FRACTIONS AND FACTORIZATION
When division involves a denominator which is not a factor of the numerator, the division gives a reminder. And therein lies the palaver of fraction.
Fractions are decimals expressed in ratios. It is a common practice to reduce fraction to their lowest terms, rather than writing them as decimals. For example: 25/10 is reduced to 5/2 rather than writing as 2.5 and so on. When an expression contains a fraction, the first approach is to compress the expression to a single fraction. And we do this with the help of the LCM of the denominators. LCM is the Lowest Common Multiple of the denominators. Below are some examples:
Example 1:
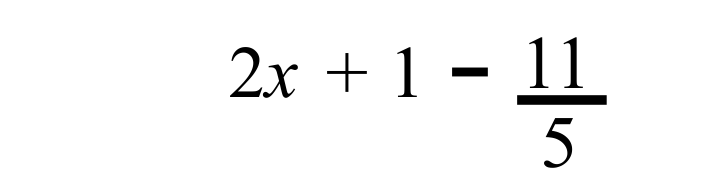
Answer:
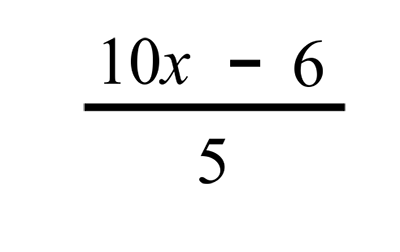
How?



Example 2:
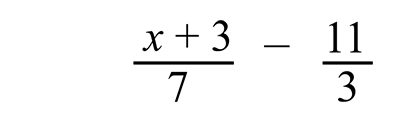
Answer:
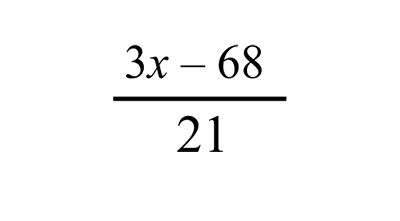
How?



FACTORIZATION
Factorization aim at reducing the terms of a mathematical expression to their lowest form via the application of HCF of the expression. Take a look at the following examples;
(1) x + 6x – 3x² (the HCF of all three is x)
(2) 2x – 8x² + 4xy (2x is the HCF)
(3) 3y + 12xy – 9xy² (3y is the HCF of all three, while 3xy is the HCF of the last two terms)
Now lets factorise the examples.







